CuPy を使った GPU 演算
ニューラルネットを実装し,テストをするためには莫大な計算量が必要になります.この全てを CPU にやらせるのは骨が折れるため,GPU を使った Python プログラミングのために CuPy の勉強をしていきます.
GPUとは
GPU とは,Graphics Processing Unit の略で,リアルタイム画像処理に特化した演算装置です.例えば,3D のゲームなどでは,ぬるぬる動く映像表現を実現するために膨大な演算が必要になります.これを担当するために使われるもので,定期的に並列な演算処理を行うことを得意とします.

上の画像のようなリアルな映像を,リアルタイムに更新していくためには常に尋常じゃない規模の計算を行う必要があります.そのため,現在の GPU の多くは高速でポリゴンの移動や回転,行列演算を行い,座標の変換やフィルタ…と様々な演算が可能なように進化しています.
最近では,GPU が多数のデータに対して並列的に (単純な) 数値計算をくり返し適用可能であることに着目して,データサイエンスなどに利用する GPGPU と呼ばれるものも登場しています.これを利用することにより,CPU (通常,コンピュータが演算処理に使うもの) ベースで動くコンピュータより遥かに早く計算をさせることが可能なため,ニューラルネットの実装には欠かせない技術になります.
CPUとの違い
CPU (Central Processing unit) とは,コンピュータの中枢を担う演算装置で,大脳のようなものです.PC でプログラムを実行する際にも,特に特別なことをしない限りは演算は全て CPU によって行われます.GPUがグラフィックに特化して仕事をしているのに対し,CPU はコンピュータ全体の処理を担当します.HDD や OS,キーボードやマウスなど,ありとあらゆるところから送られてくる情報をまとめて処理するものです.
そんな大役を担う CPU なので,当然計算性能はすさまじく高く,複雑な処理が得意です.しかしその一方,複雑な計算に耐えるように設計されているので単純な計算だろうと堅実に,順番に取り組むので,時間がかかってしまう傾向があります.コアと呼ばれる実行単位のようなものも少ないため,大量に計算を投げつけられるのが苦手です.
以下,CPU と GPU の違いを確認してみます.
役割
- CPU … 全ての演算処理
- GPU … グラフィック専門
得意とする演算処理
- CPU … 連続的で複雑な演算処理
- GPU … 並列的な単純な演算処理
コア数
- CPU … 数個程度
- GPU … 数千個
実行時間
- CPU … 大規模な計算を投げられると遅い
- GPU … CPU の数倍から 100 倍以上の速度も可能.ただしコア 1 つだと CPU に遥かに劣る.人海戦術が強み.
と,このように大規模なニューラルネットを実装使用と思った時も,CPUよりGPUの方が計算に向いていることが分かります.ニューラルネットの各ニューロンで行われる計算は一つ一つは大した事ありませんが,それが何百個も集まり,さらに多層になりと,計算量が増えていくにつれて GPU のありがたみが生きてきます.
CUDA
そんなGPUですが,製造の大手企業に NVIDIA 社があります.NVIDIA は,自社製の GPU を使って汎用の演算処理を行うための実行環境として,CUDA を提供しています.このご時世ならだれもが知っている名前です.せめて10年前に株を買っておけば…
自分の環境で,本来なら CPU が行うはずの計算を GPU に投げて肩代わりしてもらうためには,これが必要になります.導入方法については環境構築にて説明しました.
更に,この CUDA を Python から呼び出す方法として CuPy を導入していました.

Python でやる時には,基本的にはこの CuPy の使い方をマスターすれば良いわけですが,そもそも CuPy を使うために CUDA の知識が多少必要になるっぽいので確認していきます.
ここではまず CUDA について理解するために直接いじってみます.CUDA プログラミングは,C 言語ベースになっているようです.あまり慣れていないので面倒だけど,行列の積を解く問題を考えます.参考はこちら.
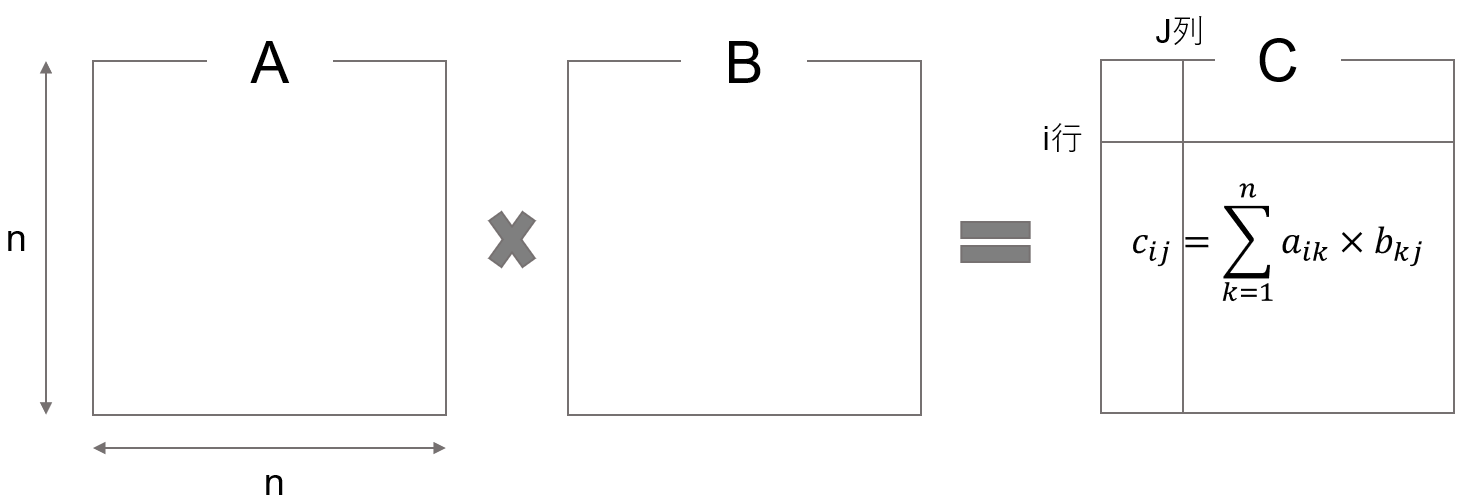
画像のような問題は,C 言語だと以下のようになります.
1
2
3
4
5
for (i = 0; i < n; i++) { // i行目,
for (j = 0; j < n; j++) { // 第j列に注目
for (k = 0; k < n; k++) { // 次元数分,下の計算をやる
c[i][j] += a[i][k]*b[k][j]; // cijはaikとbkjの積
} } }
この計算を,CPU に行わせると,次元数に応じてかなり大きな回数の計算を行うことになるため,時間がかかってしまいます.ここで GPU の出番です.GPU は,性能は低いけども計算が可能な演算装置,コアがたくさんいます.こいつらにそれぞれ,自分の担当の $C_{ij}$
1
2
3
for (k = 0; k < n; k++) { // 次元数分,下の計算をやる
c[i][j] += a[i][k]*b[k][j]; // cijはaikとbkjの積
}
を割り振って計算してもらえば,一つ一つのコアがやる計算はとても少なくなるため,超高速化が可能になるわけです.CUDA ではこの際,分担してくれるコア達のことをスレッドと呼ぶようです.
では実際,そのような分担はどうやってやらせるのでしょうか.答えを確認すると以下のようになるようです.
プログラム全体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <stdio.h>
#include <stdlib.h>
__global__ void mm_gpu(double *A, double *B, double *C, int n)
{
int i, j, k;
i = blockIdx.y * blockDim.y + threadIdx.y;
j = blockIdx.x * blockDim.x + threadIdx.x;
// 自身の番号から担当 (i,j) を決める
if (i >= n || j >= n) return; // 行列からはみ出す部分は計算しない
for (k = 0; k < n; k++) { // 総和の計算
C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i][j] += A[i][k] * B[k][j]
}
}
int main(int argc, char *argv[])
{
int i, j, n;
double *A, *B, *C;
double *DA, *DA, *DC;
n = atoi(argv[1]); // 行列の大きさ
// A, B, Cのためにホストメモリを確保
A = (double *)malloc(sizeof(double)*n*n);
B = (double *)malloc(sizeof(double)*n*n);
C = (double *)malloc(sizeof(double)*n*n);
// A, Bの内容を設定し、Cをゼロクリア(略)
// A, B, Cのためにデバイスメモリを確保
cudaMalloc((void**)&DA, sizeof(double)*n*n);
cudaMalloc((void**)&DB, sizeof(double)*n*n);
cudaMalloc((void**)&DC, sizeof(double)*n*n);
// A, B, Cの内容を、ホストメモリからデバイスメモリへコピー
cudaMemcpy(DA, A, sizeof(double)*n*n, cudaMemcpyHostToDevice);
cudaMemcpy(DB, B, sizeof(double)*n*n, cudaMemcpyHostToDevice);
cudaMemcpy(DC, C, sizeof(double)*n*n, cudaMemcpyHostToDevice);
// GPUカーネル関数を呼び出す!! 約n*n個のスレッドを使う
mm_gpu<<<dim3((n+BS‐1)/BS, ((n+BS‐1)/BS)), dim3(BS, BS)>>>
(DA, DB, DC, n);
// 結果のCを、デバイスメモリからホストメモリへコピー
cudaMemcpy(C, DC, sizeof(double)*n*n, cudaMemcpyDeviceToHost);
// Cを出力などに利用(略)
return 0;
}
CUDA のプログラムは,xx.cu という拡張子で,C ベースで書かれます.これらは,概要としては
- CPU が GPU のメモリ上にデータ用領域を確保
- CPU が GPU に入力されたデータを転送
- CPU が GPU カーネル関数を呼び出し
- GPU が計算
- CPU が GPU の計算結果を CPU に送信
の段階に分かれているようです.このうち,GPU が計算する部分が一番最初の記述,
1
2
3
4
5
6
7
8
9
10
11
__global__ void mm_gpu(double *A, double *B, double *C, int n)
{
int i, j, k;
i = blockIdx.y * blockDim.y + threadIdx.y;
j = blockIdx.x * blockDim.x + threadIdx.x;
// 自分の背番号から担当する (i,j) を決める
if (i >= n || j >= n) return; // 行列からはみ出す部分は計算しない
for (k = 0; k < n; k++) { // 総和を計算する部分
C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i][j] += A[i][k] * B[k][j]に相当
}
}
に値します.この部分を GPU カーネル関数と言い,それ以外の部分をホスト関数と言います.ホスト関数は CPU 側で動くものですね.ということで,この関数,というかプログラムに対して引数として何をいれて (CPU->GPU),何を出力させるか (GPU->CPU) をよく考えることと,そのためにどんな計算領域が必要になるか,あるいは用意させるか,そして最後に,どの変数は GPU から CPU に送信するのかなどを色々と工夫することが可能になりそうです.
一般に,CPU と GPU で情報のやり取りが生じると時間がかかってしまうらしいので,たとえば A と B を引数にして C を算出するプログラムを考えた場合,GPU からは C だけ送られれば十分なので A と B は送らないといったことをすると高速化できるそうです.
このあたりは
1
2
3
cudaMemcpy(DA, A, sizeof(double)*n*n, cudaMemcpyHostToDevice);
cudaMemcpy(DB, B, sizeof(double)*n*n, cudaMemcpyHostToDevice);
cudaMemcpy(DC, C, sizeof(double)*n*n, cudaMemcpyHostToDevice);
の記述が関係するらしいです.引数は順に,転送先,転送元,サイズ (?),Host (CPU) から Device (GPU) なのか,あるいはその逆か,の 4 つになります.この例では,CPU から GPU に 3 つの変数を送っています.ここら辺については,また必要になったら掘り下げていきます.
次に,GPU にどれだけのスレッドを使わせるかを指定する記述です.
1
2
3
// GPUカーネル関数を呼び出す!! 約n*n個のスレッドを使う
mm_gpu<<<dim3((n+BS‐1)/BS, ((n+BS‐1)/BS)), dim3(BS, BS)>>>
(DA, DB, DC, n);
mm_gpu は関数の名前で,<<<>>> が使用するスレッドの数の指定になるようです.これもよく分からない.(DA,DB,DC,n) は関数に渡したい引数のようですね.いずれにせよ,ここの記述によって,どれだけスレッドを使用するのか,(= どれだけ GPU に頑張らせるのか) を指定できるようです.
ともかく,これで呼び出された関数が
1
2
3
4
5
6
7
8
9
10
11
__global__ void mm_gpu(double *A, double *B, double *C, int n)
{
int i, j, k;
i = blockIdx.y * blockDim.y + threadIdx.y;
j = blockIdx.x * blockDim.x + threadIdx.x;
// 自身の担当する (i,j) を決める
if (i >= n || j >= n) return; // 行列からはみ出す部分は計算しない
for (k = 0; k < n; k++) { // 総和
C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i][j] += A[i][k] * B[k][j]に相当
}
}
ということになりそうです.解読します.
まず,最初の __global__ は GPU カーネル関数の印です.そして void 以降が関数の定義で,関数名および引数の指定をしています.
次に int である i と j を使って,自身の担当する要素を指定しています.block やら thread やらが出てきてよく分かりませんが,とりあえずこれがそれぞれの割り当てになります.
それぞれのスレッド? の担当が決まったら,あとはそれに合わせて計算を割り振るだけです.
それぞれの計算機に課される仕事は,自身の担当する $C_{ij}$ を計算することです.このサンプルコードだと ABC の形は n*n の長さをもった 1 次元配列の形を取っているので,たとえば $C_{ij}$ は C[i*n+j] でアクセスできます.
ということで
1
2
3
for (k = 0; k < n; k++) { // 総和
C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i][j] += A[i][k] * B[k][j]に相当
}
つまり
\[C_{ij} = \sum_{k=0}^{n-1} A_{ik} \times B_{kj}\]をするだけとなります.
CPU の場合は,一つの計算機というか単位が計算を担当するため,順番に処理しないといけなくなり,実装としては
1
2
3
4
5
for (i = 0; i < n; i++) { // i行目,
for (j = 0; j < n; j++) { // 第j列に注目
for (k = 0; k < n; k++) { // 次元数分,下の計算をやる
c[i][j] += a[i][k]*b[k][j]; // cijはaikとbkjの積
} } }
のように 3 重のループ構造になっていました.このうち,2 つのループをなくして別々のユニットに計算させるのが CUDA プログラムのメリットでした.
CuPy
以上のように,CUDA を使った GPU プログラミングの基本がなんとなく読めてきたところで,本題の CuPy の使い方を確認します.
CuPyとは
CuPy は Preferred Networks 社が開発しているオープンソースの高速な行列計算ライブラリです.中身としては,NumPy の GPU 版のようなもので,基本的には NumPy ベースで動くプログラムであれば np を cp に変えるだけで動いてくれます.
DeepLearning のフレームワークである Chainer のバックグラウンドでも動いているようです.

CuPyによるNumPyの互換プログラム
まずは軽く使い方を確認していきます.Git の方のコードは CuPy.ipynb です.
まずは必要なライブラリの import から.
code
1
2
3
4
5
import numpy as np
import cupy as cp
from skimage import data,transform,color,io
import time
次に,性能評価をするためにフーリエ変換にかける画像を読み込みます.
code
1
2
3
4
5
6
7
8
np_img = data.astronaut()#画像ロード
np_img = color.rgb2gray(np_img)#グレースケール化
np_img = np_img.astype('f')
io.imshow(np_img)#画像の表示
cp_img = cp.asarray(np_img)#numpy配列をcupy配列に変換
ここで,numpy で定義した配列を cupy 配列に変換するためには cp.asarray 関数を使用します.これをあまりやりすぎると計算が遅くなるので極力 for には含みません.
では早速,計算性能の比較をしていきます.まずは NumPy,つまり CPU で計算させる普通のプログラムです.
code
1
2
3
4
5
6
7
8
9
10
11
12
times_cpu = [] # CPUの計算時間保存用
for N in [10,100,1000,10000]:
time_start = time.time()
for i in range(N):
sainokawara = np.fft.fft(np.fft.ifft(np.fft.fft(np_img)))
time_end = time.time()
elapsed_time = time_end - time_start # 経過時間
times_cpu.append(elapsed_time)
同様に CuPy も.
code
1
2
3
4
5
6
7
8
9
10
11
12
times_gpu = [] # GPUの計算時間保存用
for N in [10,100,1000,10000]:
time_start = time.time()
for i in range(N):
sainokawara = cp.fft.fft(cp.fft.ifft(cp.fft.fft(cp_img)))
time_end = time.time()
elapsed_time = time_end - time_start # 経過時間
times_gpu.append(elapsed_time)
CuPy は NumPy の np を cp に変換しただけです.これで計算が済んだので,結果を比較してみます.
code
1
2
3
4
5
6
7
8
9
10
11
12
13
import tabulate
# N ごとの実行時間の差
N = [10, 100, 1000, 10000]
times_cpu = np.asarray(times_cpu)
times_gpu = np.asarray(times_gpu)
# tabulate を用いてテーブルを作成
table = tabulate.tabulate(
zip(N, times_cpu, times_gpu),
headers=['N', 'NumPyでの実行時間 (sec)', 'CuPy での実行時間 (sec)'])
print(table)

圧倒的に CuPy の方が早いことが確認できました.NumPy 自体が行列演算に特化したライブラリなので,それをさらに GPU で行うためにこのように早くなるわけですね.CUDA のプログラムを書かなくても GPU が利用できるのはとても便利です.
ちなみに,この速さはあくまで cp(np) を使った演算をしているからですので,同じように行列の演算であっても np を使わない実装をしていた部分に関してはむしろ遅くなってしまいます.
たとえば,for で回しまくっていたプログラムであれば,これを GPU に投げ渡してしまうと1つのユニット,それも CPU よりも貧弱な計算能力のものに全て計算を任せるわけですから,途方もない時間かかってしまいます.
従って,CuPy ベースのプログラムでは,cp 関数での計算以外は高速化できないことになります.
たとえば,自分が書いていたコードですが
1
2
for post_neuron in range(len(self.x)):
self.W[post_neuron] += self.learning_rate * (self.x[post_neuron] * self.x - cp.square(self.x[post_neuron]) * self.W[post_neuron])
という記述が,逐次的に呼び出されていた場合,cupy を使うことでむしろ遅くなります.これが仮に
1
2
for post_neuron in range(len(self.x)):
cp.dot(a,b)
のような記述だったら早かったはずです.しかし,これではやや不便です.numpy の関数にない計算をさせたいことだってたくさんあります.
CuPy.ElementwiseKernel
np を cp に変えるのは,CPU に最適化された実装から GPU に最適化された実装への変換を意味します.
しかし,そもそも CPU への最適化も難しく,あるいは開発者の頭が足りず,Python の for ループで頑張って実装していた部分を GPU で早くしたい.というモチベーションもあり得ます.
そんな時につかうのが CuPy の ElementwiseKernel という機能で,CUDA の GPU カーネルの中身を直接書いて CUDA を呼び出すことが出来ます.
メリットとして,上で見てきたようにブロックやスレッドの数,メモリ管理のようなよく分からなかった部分は触らず (勝手に調整してくれる) に,GPU にやってもらいたい計算部分 (=GPUカーネル関数) のみを書けるということがあります.
やっていきます.
まずはシンプルに,二つの正方行列の和を計算させます.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
X = cp.arange(25).reshape(5, 5)
Y = cp.arange(25).reshape(5, 5)
# ありものの関数で計算
arimono = cp.add(X,Y)
# カーネル関数を定義、生成
mat_add_kernel = cp.ElementwiseKernel(
in_params='int32 x, int32 y', # input parameterを指定する.型の指定は必要.
out_params='float32 z', # output parameterの指定.
operation=\ # 実行する関数の中身を記述する.これでnpにないものも使える
'''
z = x + y;
''',
name='mat_add_kernel') # 関数名
# カーネル関数の呼び出し
Z = mat_add_kernel(X, Y)
print('cp.add = \n', arimono)
print('carnel = \n', Z)
てきとうに,X と Y の2つの正方行列を定義し,その和を計算させています.
この程度であれば,numpy および cupy の .add 関数で計算可能ですので,ひとまずさせておいて,自分で実装したものと計算結果を比較してみます.
実装の詳細はとりあえず省き,結果を出してみると

と一致していることが分かります.型は違っていますが,わざとです.とりあえず,CuPy.ElementwiseKernel で普通の cp 関数を再現できることが確認できました.
では実際の実装について見ていきます.
1
2
3
4
5
6
7
8
9
10
11
12
# カーネル関数を定義、生成
mat_add_kernel = cp.ElementwiseKernel(
in_params='int32 x, int32 y', # input parameterを指定する.型の指定はしないとっぽい.Cだからかな
out_params='float32 z', # output parameterの指定.
operation=\ # 実行する関数の中身を記述する.これでnpにないものも使える
'''
z = x + y;
''',
name='mat_add_kernel') # 関数名
# カーネル関数の呼び出し
Z = mat_add_kernel(X, Y)
GPU に関連するのはこの部分だけです.11,12 行目は,それ以前で定義した関数を呼び出しているだけなので,中身自体は 9 行です.CuPy.ElementwiseKernel でのカーネル関数の定義には 4 つの要素が必要になるようなので,順に確認していきます.
- in_params
- out_params
- operation
- name
まず,in_params は引数です.この関数を呼び出すさいに用いる変数ですね.12 行目で関数を呼び出す際,X と Y が引数として与えられています.関数の定義時には,この関数がどういった値を受け取って動作するのかを型とともに指定してやる必要があります.Cっぽいですね.ここでは,正方行列の定義は普通に整数値だったので int32 を型として,2つの引数がくると定義しました.
次に,out_params です.こちらはそのまま,出力されるパラメータの定義ですね.12 行目で呼び出された後はZに格納される値の定義です.単純に int 同士の和なので int で良いですが,型の指定が大事ってことを強調するために float にしてみました.実際結果を見てみても,kernel 関数にやらせた方では出力の値が float になっていたと思います.
次,operation ですが,ここに具体的な計算の内容を記述することになります.今回は行列の和なので単純に足し算だけ書いています.
最後にnameですが,こちらは関数の名前です.といっても,1行目でも既に指定しているのでよく分かりません.必要なんですかねこれ.
配列のindexing
個人的に,GPU を使いたくなった理由は自作のニューラルネットワークにシナプス可塑性を導入した際,膨れ上がった計算時間を短縮することでした.シナプスの繋がりは,細胞数の二乗になるため,
1
2
3
4
5
for t in range(入力刺激の長さ):
# リザバー結合重み行列の更新
for post_neuron in range(ニューロン数):
for pre_neuron in range(ニューロン数):
W[post_neuron, pre_neuron] += 増加分(仮にX[post]*X[pre])
正確なコード
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 変数
T = 500 # 入力時系列の長さ
N_x = 200 # 中間層の数
N_in = 1 # 入力層の数
N_out = 1 # 出力層の数
activation_func = np.tanh # 活性化関数
learning_rate = 0.000001 # 可塑性の学習率
np.seed = np.random.seed(seed=0)
# 入力時系列データ
U = np.random.randn(T,1)
# 入力から中間層への結合重みの初期化
Win = np.random.uniform(-1,1,(N_x, N_in))
# 中間層の状態ベクトルの初期化
x = np.zeros(N_x)
W = np.random.uniform(-1,1,(N_x, N_x))
train_len = len(U)
# 時間発展
for n in range(train_len):
x_in = np.dot(Win, U[n])
x = x + activation_func(np.dot(W, x) + x_in)
# リザバー結合重み行列の更新
for post_neuron in range(N_x):
W[post_neuron] += learning_rate * (x[post_neuron] * x - np.square(x[post_neuron]) * W[post_neuron])
# リザバー結合重み行列の更新(for 書き下し)
#for post_neuron in range(N_x):
# for pre_neuron in range(N_x):
# W2[post_neuron, pre_neuron] += learning_rate * (x[post_neuron] * x[pre_neuron] - np.square(x[post_neuron]) * W2[post_neuron, pre_neuron])
のような実装が必要になります.このような多重 for 文は cupy にそのまま渡してしまうと計算が重くなりすぎるので,elementwisekernel を使って上手く計算させる必要があります.
1
2
3
4
5
6
7
8
9
hebbian = cp.ElementwiseKernel(
in_params='float64 W, float64 X',
out_params='W',
operation=\
'''
W[post][pre] += x[post] * x[pre];
''',
name='hebbian')
のような実装を目指します.
ここで X はニューロンの状態ベクトル,W はその組み合わせ間のシナプス結合重み行列です.たとえば $W_{32}$ は 2 個目のニューロンから 3 個目のニューロンへの結合重みです.この重みを hebb 則に従って調整するためには,シナプス前細胞と後細胞の活動を,配列 W のインデックスに従って参照する必要があります.
cp.ElementwiseKernel では,添え字アクセスを使うには,引数の指定の際に raw をつけます.これによって,指定した引数に対し特殊変数 i を使うことが出来るようになります.
また,インデックス処理の際には出力する配列の大きさは先に決めておく必要があるようです.それに関係し,関数の呼び出しの際にも引数として出力変数を指定します.
挙動を確認してみます.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
X = cp.zeros(25).reshape(5, 5).astype(cp.int16)
Y = cp.zeros_like(X) # yにあらかじめ出力の入れ物を用意
Z = cp.zeros_like(X) # yにあらかじめ出力の入れ物を用意
kernel = cp.ElementwiseKernel(
in_params = 'raw int16 X, int16 shift, int16 width', # x に raw を指定
out_params = 'int16 Y, int16 Z',
operation=\
'''
Y = X[i]+shift;
Z = i;
''',
name='kernel')
kernel(X,2,X.shape[1],Y,Z) # 引数に出力も追加しなければならない
print('Y = \n', Y)
print('Z = \n', Z)
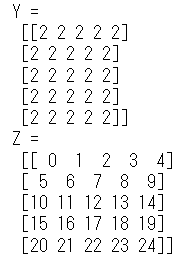
上のコードでは,5*5 に並んだ 0 の配列 X が与えられ,index を取得しています.これを利用し,X の各要素 (といっても 0 ですが) に 2 を足したものをY としました.ここまでは普通です.
次にZですが,こちらは X から取得した index そのものの配列です.中身を確認してみると,0 から 24 の数字が振られています.raw による indexing は行を無視した通し番号になるということですね.
これにより,多次元配列での実装で (x,y) にアクセスしたいなどといった際には多少工夫が必要です.
Oja’s hebbian ruleの実装
以上の勉強内容を踏まえて,冒頭のシナプス可塑性を実装してみたのが以下の記述です.
1
2
3
4
5
6
7
8
9
10
11
kernel = cp.ElementwiseKernel(
in_params = 'raw float64 W, raw float64 x, int16 width, float64 learning_rate',
out_params = 'raw float64 W_new',
operation=\
'''
int x_idx = i%width; // pre synapse
int y_idx = i/width; // post synapse
W_new[i] = learning_rate * (x[y_idx]*x[x_idx] - x[y_idx]*x[y_idx]*W[i]);
''',
name='kernel')
入力として,
- 可塑性が効く前の結合重み行列 W
- ニューロン状態ベクトル x
- ニューロンの個数 width
- 学習率 learning_rate
を読み込み,出力として
- 可塑性が効いた後の結合重み行列 W_new
を排出しています.このうち,結合重み行列から index を取得し,行と列からそれぞれシナプス前後のニューロンの指定を行うために x_idx y_idx を定義しました.これらを用いて,Oja の Hebbian rule に従って差分を計算する関数です.main のプログラムは
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
kernel = cp.ElementwiseKernel(
in_params = 'raw float64 W, raw float64 x, int16 width, float64 learning_rate',
out_params = 'raw float64 W_new',
operation=\
'''
int x_idx = i%width;
int y_idx = i/width;
W_new[i] = learning_rate * (x[y_idx]*x[x_idx] - x[y_idx]*x[y_idx]*W[i]);
''',
name='kernel')
# 変数
T = 500 # 入力時系列の長さ
N_x = 200 # 中間層の数
N_in = 1 # 入力層の数
N_out = 1 # 出力層の数
activation_func = cp.tanh # 活性化関数
learning_rate = 0.000001 # 可塑性の学習率
cp.seed = cp.random.seed(seed=0)
# 入力時系列データ
U = cp.random.randn(T,1)
train_len = len(U)
# 初期化
Win = cp.random.uniform(-1,1,(N_x, N_in)) # 入力結合重み行列
x = cp.zeros(N_x) # ニューロンの状態ベクトル
W = cp.random.uniform(-1,1,(N_x, N_x)) # 中間層結合重み行列
W_new = cp.zeros_like(W) # kernelのための入れ物
for n in range(train_len):
# ニューロン状態の更新
x_in = cp.dot(Win, U[n]) # 入力の読み込み
x = x + activation_func(cp.dot(W, x) + x_in) # ニューロン更新
# リザバー結合重み行列の更新
W += kernel(W,x,W.shape[0], learning_rate, W_new, size=(W.shape[0] * W.shape[1])) # 引数に出力も追加
のようになります.
確認
不安になったので,一応 numpy の実装と同じ挙動なのかを確認します.Numpy と Cupy は random 関数の seed が異なる値になるようなので,
- numpy で計算した結果
- numpy で生成した配列を cp に変換してから計算した結果 が等しいかどうかを確認します.
Numpy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 変数
T = 500 # 入力時系列の長さ
N_x = 200 # 中間層の数
N_in = 1 # 入力層の数
N_out = 1 # 出力層の数
activation_func = np.tanh # 活性化関数
learning_rate = 0.000001 # 可塑性の学習率
np.seed = np.random.seed(seed=0)
# 入力時系列データ
U = np.random.randn(T,1)
# 入力から中間層への結合重みの初期化
Win = np.random.uniform(-1,1,(N_x, N_in))
# 中間層の状態ベクトルの初期化
x = np.zeros(N_x)
W = np.random.uniform(-1,1,(N_x, N_x))
train_len = len(U)
# 時間発展
for n in range(train_len):
x_in = np.dot(Win, U[n])
x = x + activation_func(np.dot(W, x) + x_in)
# リザバー結合重み行列の更新
for post_neuron in range(N_x):
W[post_neuron] += learning_rate * (x[post_neuron] * x - np.square(x[post_neuron]) * W[post_neuron])
# リザバー結合重み行列の更新(for 書き下し)
#for post_neuron in range(N_x):
# for pre_neuron in range(N_x):
# W2[post_neuron, pre_neuron] += learning_rate * (x[post_neuron] * x[pre_neuron] - np.square(x[post_neuron]) * W2[post_neuron, pre_neuron])

Numpy -> Cupy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
kernel = cp.ElementwiseKernel(
in_params = 'raw float64 W, raw float64 x, int16 width, float64 learning_rate',
out_params = 'raw float64 W_new',
operation=\
'''
int x_idx = i%width;
int y_idx = i/width;
W_new[i] = learning_rate * (x[y_idx]*x[x_idx] - x[y_idx]*x[y_idx]*W[i]);
''',
name='kernel')
# 変数
T = 500 # 入力時系列の長さ
N_x = 200 # 中間層の数
N_in = 1 # 入力層の数
N_out = 1 # 出力層の数
activation_func = cp.tanh # 活性化関数
learning_rate = 0.000001 # 可塑性の学習率
np.seed = np.random.seed(seed=0)
# 入力時系列データ
U = np.random.randn(T,1)
U = cp.asarray(U)
# 入力から中間層への結合重みの初期化
Win = np.random.uniform(-1,1,(N_x, N_in))
Win = cp.asarray(Win)
# 中間層の状態ベクトルの初期化
x = cp.zeros(N_x)
W = np.random.uniform(-1,1,(N_x, N_x))
W = cp.asarray(W)
train_len = len(U)
W_new = cp.zeros_like(W)
for n in range(train_len):
x_in = cp.dot(Win, U[n])
x = x + activation_func(cp.dot(W, x) + x_in)
# リザバー結合重み行列の更新
W += kernel(W,x,W.shape[0], learning_rate, W_new, size=(W.shape[0] * W.shape[1])) # 引数に出力も追加

一致しています.無事に CPU のプログラムを GPU に変換できています.
速度比較
結果,どれだけ早くなるのかを確認します.
1
2
3
4
5
6
7
8
9
10
11
12
13
import tabulate
# N ごとの実行時間の差
T = [500,5000,44100]
times_cpu = np.asarray(times_cpu)
times_gpu = np.asarray(times_gpu)
# tabulate を用いてテーブルを作成
table = tabulate.tabulate(
zip(T, times_cpu, times_gpu),
headers=['T(length of input)', 'CPU での実行時間 (sec)', 'GPU での実行時間 (sec)'])
print(table)
まず,入力時系列の長さを変化させていった時のCPU,GPUそれぞれの計算時間を比較します.

次に,同様にニューロンの数を変化させて比較します.
code
1
2
3
4
5
6
7
8
9
10
11
12
13
import tabulate
# N ごとの実行時間の差
N = [200,1000,2000]
times_cpu = np.asarray(times_cpu)
times_gpu = np.asarray(times_gpu)
# tabulate を用いてテーブルを作成
table = tabulate.tabulate(
zip(N, times_cpu, times_gpu),
headers=['N(Size of reservoir)', 'CPU での実行時間 (sec)', 'GPU での実行時間 (sec)'])
print(table)

どちらも,GPU を使うことで計算時間が大幅に短縮されているのが確認できました.