掛け算
脳波の解析などに使用する数学はどれも大学レベルのものとなります.しかし,筆者がそうだったように,そもそも高校数学からあまりまともに取り組んでこなかった人や,文系だったために履修すらしていないという方も一定数いると思います.
高校レベルの知識がない状態で学べる程,数学は簡単ではありません.筆者のように時間を無駄にしないためにも,まずは基礎から復習していきます.
以降の章でやっていく内容を読んでいく上で最低限覚えておいてほしい内容です.
ただ,どの項目についても言えることですが,
多少なりとも数学慣れしている人には退屈だろうと思うので,飛ばしてください.
様々な「数」の形と,その掛け算
これから,信号処理や統計といった難しい数学をこれから皆さんはやっていくわけですが,こういった数学は結局のところどこまで行っても足し算と掛け算です.
脳波の解析も統計も基本的には,出てくる数式は複雑な「数」に対応した,複雑な「足し算,掛け算」をしていく処理にすぎません.なのでまずはここで,掛け算とは何かを考えていきましょう.足し算については比較的簡単であまり違いを意識しなくても良いので,ここでは掛け算のみ触れます.
まず理解しないといけないのは,世の中には色々な「数」があって,対応した色々な「掛け算」がある.という事です.まずはこの事をしっかり頭に入れておけば,解析とかの勉強もさして難しくないはずです.別に全て覚える必要はないので,とにかく色々あるんだなーとだけ感じてください.
数,というと普通に思い浮かぶのは1とか100とか,そういった数字的なものだと思います.が,これからやっていく発展的な数学においては,様々な「数」を扱っていくことになります.まずはその確認からです.世の中にはいわゆる「数」ではない「数」が存在していて,そいつらはそれぞれ別の用途で使われるどれも大事なものなのだと理解しましょう.
(厳密には,数というと複素数体 $\mathbb{C}$ の話になると思いますが,ここではベクトルなどの「数の束」も含めて紹介します.)
いわゆる数
まずはいわゆる数について考えます. 先程も確認したように,数といってパッと思いつくのは,$1$ とか $3$ とかといったものでしょうが,これは数という大きな集合のうちのほんの狭い領域です.
数の定義について,実は明確なものは(少なくとも筆者が調べる限りでは)ない…ように見えます.しかし,何が数であるかは分類出来ますので,それを確認します.
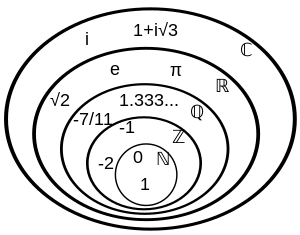
上の画像はWikipediaから拝借した,「数」を構成する様々な数についての関係を表した図です.このうち,どこまでを数として認識できるかで数学的素養が見えそうな気がしますが,筆者は勉強を始める前は「集合 $\mathbb{R}$ が入るかどうか,聞かれたらYesなんだけど,感覚的には微妙…」という程度でした.順に見ていきます.
自然数
自然数とは,図でいう集合 $\mathbb{N}$ の $0$ や $1$ のことです.いきなりちょっと違和感を覚えるかも知れないポイントですが,$0$ は大学以降,自然数として扱ったり,扱わなかったりするようです.自分は数学に真面目に取り組んでいる訳ではないのでよく分かりませんが,$0$ を自然数として扱う資料が多いような気もします.
いずれにせよ,それ以外の範囲についての定義は「$1$ と,それに $1$ ずつ加えていって得られる数」といった表現になると思います.数学的な厳密性はそこまで追求しません.
整数
整数とは,これもまた分かりやすいものですが,「$1$ と,それに $1$ ずつ加えて行って得られる自然数に加え,それに「$-1$」を乗じて得られる負の数,そして $0$」が定義です.画像では,$-1$ や $-2$ が追加されています.
このくらいまでは流石に,確認する必要もなかったでしょうか.
有理数
ここら辺から,知ってはいるけど定義が何になるのかちょっとあやふやになってきます.有理数とは整数に,いわゆる「分数」を追加したものでした.たとえば$\frac12$なんかも含むものです.
しかしここでは,もう少し丁寧に書きます.
\[\mathbb{Q} = \{\frac{a}{b} | a,b \in \mathbb{Z}, b\neq0\}\]が有理数の定義です.集合の記号に慣れていないと思うので日本語で書くと, 「整数 $a,b$ の商の形で表せる数の集合.ただし分母に来る $b$ は $0$ でないものとする」 といったところでしょうか.つまり,分数として表すことが出来る数ということです.$0$ は割り算に使えないので,省く必要があるわけですね.
実数
もう少しです.実数 $\mathbb{R}$ とは,有理数に,有理数ではない数である無理数を加えた数の集合になります.よく分かりませんね.しかし,目的を考えれば何故この数を考える必要があるのか,なんとなくの理解は出来ると思います.
よく言う話に,円周率 $\pi=3.1415\dots$ は分数で表すことが出来ないというものがあります.しかし $3.14\dots$と数で書けることからも明らかなように,たしかに存在するはずです.有理数しか考えられない場合,無理数によって生じるこうした「飛び地」によって数直線を書こうと思っても書けなくなってしまうのです.
直線とは,途切れることなく連続した線です.なので,飛び地はなくす必要があります.そこで考えられたのが無理数を含むことで途切れることなく線を描けるようになった実数です.
複素数
実数までは,足し算や掛け算のやり方も基本的には同じなので分かりやすかったと思います.強いて言うなら,無理数である $\pi$ や $\mathrm{e}$ は数字で表すことが出来ないので,たとえば
\[1+2 = 3\\ 3 \times -\frac{4}{3} = -4\]のように計算をすることが出来ず,
\[\begin{align} \pi + \mathrm{e} = \pi + \mathrm{e}\\ 5 \times \pi = 5\pi \end{align}\]のような表記になるところくらいでしょうか.しかしこれでも,やっている計算処理そのものは同じです.複素数まで拡張するとなると,こう上手くも行かなくなってしまいます.
しかし複素数は,脳波解析のような信号処理を学ぶ上で必須の概念となりますので,後ほど詳しく学びます.
とにかく,ここまでにまとめた自然数~複素数まで拡張可能な集合を,一般には「数」と称しているようです.
複数の「数」からなる「数」の形
では,数学で扱う「数」的なもの,つまり足し算や掛け算の対象にするものはこれだけなのかというと,違います. (重ねて言い訳ですが,ここでの「数」は数学的定義とは離れます.演算の対象になるもの,くらいのイメージです)
様々な数学的操作を楽に行うため,人類はこれまでに確認した数に加え,「複数の数からなる数」 も扱います.意味が分からないと思うので確認をしていきます.とは言っても,複数の数からなる数には様々なものがあります.
- ベクトル
- 複素数
- 行列
等です. 複素数については上で存在だけ確認もしました.これらを対象とした足し算や掛け算は,自然数や実数の掛け算とは全く違う演算になります.
筆者含め,多くの高校生は「こんなわけわからないものを考えて何の意味があるのか」と思うはずです.そして大学に入ってから必要性に気付いて復習するまでがテンプレです.
高校以上の数学は非常に難しいもので, 僕も全く分からずに置いて行かれましたが, どうにか理解するための最初の第一歩は,
「世の中には(自分の思っていた)数じゃない数があるらしい」
と知る事です. 僕はこれを理解するまでに無駄に長い時間を費やしてしまいました.
では, そもそも何故そんな数を考える必要があるのでしょうか?
言い換えると,何故先程確認した実数の形以外の数や,その表記,それぞれに対応した演算方法を考える必要が出てくるのでしょうか? その答えは,実数は結局のところ1本の数直線上の点の集合に過ぎないからです.
$0$ があって $1$ があり, その次に $2$ が来るのは小学2年生の数直線ですが, 小学4年生頃には「どうやら $0$ と $1$ の間にも小数や分数があるらしい」と知ります. 次に中学になり, $0$ の向こう側には同じだけの数の負の数があり, 更には √ がつく数などもある事を知ります. そして少し飛びますが高校では, 数直線の右と左に終わりはなく, 無限という領域に飛んでいる事を知りますね. ここまでが実数の学習順序ですが, いずれも 1 本の直線を細かく見たり, あるいはずっと先を見ているだけです.
これだけでは記述できる情報が少ないため, 不都合があるから別の数を考える必要があったわけです. これまでに定義してきた数を,いろんなやり方で複数束ねてまとめた「数」を新しく定義してやれば表現できる情報量は各段に増え, 世界が広がります.
1次元より2次元,2次元より3次元の方が情報が多く,表現が広がるのは直観的にも明らかですね.
ベクトルの積
ベクトルの定義
ベクトルの定義は,高校数学では「向きと大きさをもった量」でしょうか.よく矢印を使って表されるものです.たとえば,
\[\begin{pmatrix} 1 \\ 2 \end{pmatrix}\]などですね.これを平面上に置くとしたら,右に $1$,上に $2$ といった量です.とは言え,これだけの定義だと平面上のどこに置くかの指定がないです.物理とかで使う分にはその方が便利ですが,座標を固定して,$(0,0)$ からどれだけ離れるか,といった表現で使うことも多いです.
大学数学でのベクトルの定義は,ベクトル空間の元ということになり,やや難しくなるかも知れませんが,我々は数学を厳密に学びたいわけではないので,ひとまず置いておきます.
とにかく,そんな複数の数を束ねた数の形のひとつがベクトルです.ベクトルとは, 二次元の場合は2つ, 三次元の場合は3つの数…を束ねたものです.
なので,これまでに学んだ「数」の定義を踏まえると,以下のようなものは全てベクトルとして扱うことが出来るようになります.
- 実数を $n$ 個並べたもの … 「数」が $n$ 個並んでいるため.$n$ には $1$ も含む. \(3, \qquad \begin{pmatrix} 1\\2\\3 \end{pmatrix}, \qquad \begin{pmatrix} 2, 4, 6 \end{pmatrix}\)
- 複素数を $n$ 個並べたもの … 「数」がn個のため.\(n$ には $1$ も含む.\)3+4i, \qquad \begin{pmatrix} 1+2i\2-i\3i \end{pmatrix}, \qquad \begin{pmatrix} 2i, 4+i, 6-3i \end{pmatrix} $$
- 数列 … 「数」が無限個 (あるいは任意の個数) 並んでいるため. \(x_1,x_2,x_3\dots,x_n\)
- 関数 … $y=ax$ であれば,「数」である $x$ に対応した $y$ が無限個並んでいるため. \(y = ax+b\\ f(x) = \sin\theta\)
と言っても,最初の例以外は馴染みもなく,あまりスッと受け入れられないかも知れません.そのあたりはおいおい触るとして,まずは最初の,実数 $n$ 個の例から考えます.
数を複数束ねると, その値の間に比が生まれ,それらによって定義される長さを持った線生まれます.
これが先述した, 数を束ねたことによって増える情報量であり, ただの実数との決定的な違いになります.ベクトル $(a,b)$ は $a$ と $b$ という要素をもつだけでなく,それらの長さの比から計算されるノルム,角度が定義されるということです.
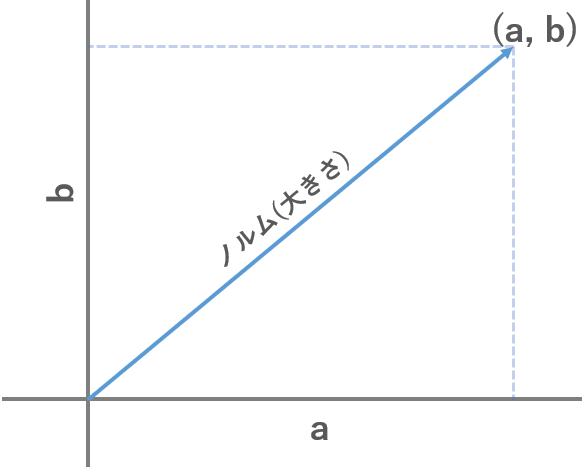
ちなみに, この「比と角度(と長さ)」の考え方ですが, これは脳波においては位相や電位の強度といったものを考える時に必要になります.図を眺めてよく確認しておきましょう.$a$ と $b$ という二つの数を束ねることによって,斜めに角度と長さをもった新たな数というか情報を表現できていますね.
ベクトルの掛け算
ベクトル同士を掛け合わせるとき, どうするでしょうか? 実は面倒なことに,ベクトル同士の掛け算にはいくつかの種類があります.数の束なので,どの数同士をかけるのかだったり,かけた後にベクトルの形でまとめるのか,あるいは一つの数に落とし込むのか,といった違いです.
ここでは,一番素朴な形を確認します.
\[(x_1 , x_2)(y_1 , y_2 ) = (x_1 y_1 + x_2 y_2)\]これをベクトルの内積と言います.
ベクトルの内積というと,覚えている人は覚えているかもしれませんが,もう一つの算出方法がありました.高校の数Bだったかの内容を思い出しましょう.
2つのベクトルの絶対値の積に互いになす角の $\cos$ をかけたものです.
\[\mathbf{a}\cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta\]まず,記号の確認からしておきます.太字は数学ではベクトルを表します.なので $\mathbf{a, b}$ は単なる数じゃないことに注意してください.
次に,$|k|$ という記法は,$k$ の絶対値を意味します.$|-3| = 3$ です.ベクトルでの絶対値の計算は大丈夫でしょうか.上の図でいうノルムの長さになります.なので,三平方の定理を使って
\[\mathbf{a} = (a_1, a_2)\\ |\mathbf{a}| = \sqrt{(a_1^2 + a_2^2)}\]として計算できます.
要素の確認が出来たので,ここからベクトルの内積について理解していきます.非常に大切なところなので丁寧に行きましょう.
普通はベクトルの内積の式を見ると,ベクトルの絶対値同士の積に,$\cos\theta$ をかけていると思うでしょうが,この解釈だと感覚的にはあまり納得できません.
そこで $|\mathbf{a}|$ に $|\mathbf{b}|\cos\theta$ をかけていると捉えてみます.もちろん $\mathbf{a}$と$\mathbf{b}$ を逆にしても大丈夫です.
では $|\mathbf{a}|$ はそのまま $\mathbf{a}$ の絶対値で良いとして,もう一つの方は一体何を表しているのかという事が当然気になるわけですが,そこで出てくるのが射影という考え方です.
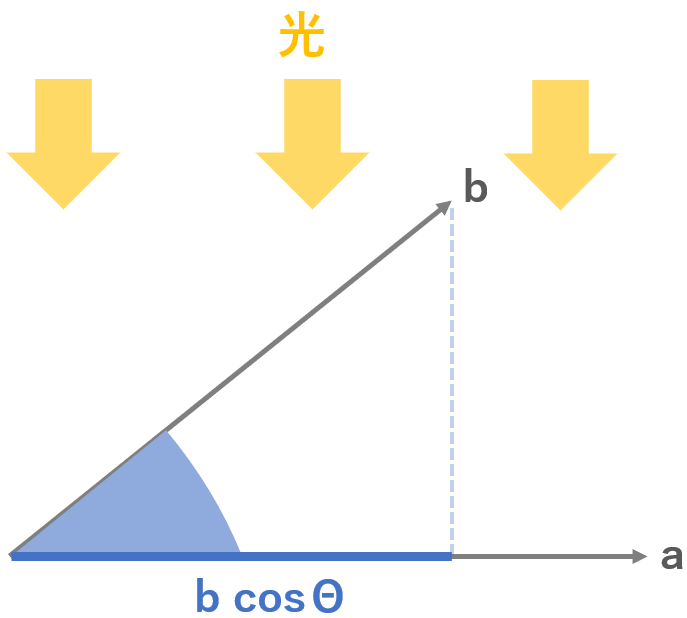
よくある説明は,ベクトル $\mathbf{a}$ に対して垂直な光によって照らされたベクトル $\mathbf{b}$ の影の長さ,というものです.つまり $|\mathbf{b}|\cos\theta$ はベクトル $\mathbf{b}$ の,ベクトル $\mathbf{a}$ の方向に対してもっている影響力とかなんかそんな感じの量です.これでベクトル同士の向きをそろえた上で,改めて $|\mathbf{a}|$ とかけているわけですね.
内積の意味
次に,ベクトルの内積というものが何を表しているのか考えてみます.
先程,内積が $\mathbf{a}$ と射影した $\mathbf{b}$ の積である事は確認できました.ここから場合分けして考えます.
まず $\mathbf{a,b}$ が同じような方向を向いていた場合,両者の間の角度である $\theta$ の値は小さくなり,射影されて出来る $|\mathbf{b}|cos\theta$ の値,即ち $\mathbf{b}$ が作る影はほぼ $| \mathbf{b}|$ から変わりません.
そこから角度が大きくなるにつれて影は短くなり,その結果内積の値も小さくなっていき,ちょうど $2$ つのベクトルが直行する時 ($\theta = \frac{\pi}{2})$ に内積は0になります($\because \cos\frac{\pi}{2}=0)$.
そしてそのまま角度を大きくしていくと,今度は射影ベクトルがベクトル $\mathbf{a}$ と全く重ならないようになってしまい,$\cos\theta < 0$ となります.つまり,二つのベクトルが直角よりなお別の向きを向いている場合,内積は負の値をとります.もはや影がベクトル $\mathbf{a}$ と反対方向に向かいつつあるからです.
この事をまとめると,以下のような関係が言えます.
内積の定義
\[\begin{align} \mathbf{a}\cdot\mathbf{b} = a_1b_1 + a_2b_2\\ |\mathbf{a}||\mathbf{b}|cos\theta \end{align}\]内積の取る値
\[\begin{align} \mathbf{a}\cdot \mathbf{b} > 0 \qquad \text{(ベクトルの向きが似てる時)}\\ \mathbf{a}\cdot \mathbf{b}=0 \qquad \text{(ベクトルが直行している時)}\\ \mathbf{a}\cdot \mathbf{b}<0 \qquad \text{(ベクトルの向きが離れている時)} \end{align}\]つまり内積とは,二つのベクトルの向きの関係性,似ているかどうかを示す指標として捉える事が出来,特に $0$ になる場合にそれらのベクトルが直行している事を示せるものです.
内積の考え方は代数学・幾何学において非常に大事になります.少し雑になりますが,脳波解析においても例えば,計測された脳波が10Hzの波にどれだけ似ているかを見ることで周波数成分を抜き出してみたりといったことに使います.
そうした処理を フーリエ変換やウェーブレット変換と言い,この基礎数学シリーズが終わって最初に学ぶ,脳波解析において最も重要な単元になります.
ベクトルの掛け算を学ぶ意味は,そもそも我々がこの先扱う事になる脳波データなどの信号は全てベクトルであるからです.これは先程のベクトルの定義で確認したように,全ての数列や関数はベクトルとして捉えられることに起因します.たとえば脳波は時間と電極の次元をもった関数なので,やはりベクトルとして扱うことになります.
勿論,ベクトルの掛け算なので他の数学にも多用されます.統計なんかでも使うごく当たり前の処理なので,ちゃんと覚えておきましょう.
複素数の積
複素数とはなんなのか,というような疑問はひとまずここでは置いてください.詳しくは,後の章で詳しく複素数について解説するとして,まずここでは「なんか不思議な数があるんだなぁ,変な掛け算の仕方だなあ」くらいを感じてもらえれば大丈夫です.
とりあえず,ベクトルと同様に複素数も平面上で捉えるとします.複素平面上では複素数は $r(\cos x + i\sin x)$ という表記で考えます.
まずはこれに対する一般的な積を考えてみましょう.
\[r_1(\cos x + i\sin x)r_2(\cos y + i\sin y) = r_1 r_2(\cos x\cos y - \sin x\sin y + i\sin x \cos y + i\cos x\sin y)\]上記は加法定理より \(r_1 r_2(\cos ( x + y) + i\sin ( x + y))\)
となります.
ベクトルの内積と似てはいますが, 決定的な違いがあります.
ノルムに対応する $r$ は普通に掛け算されているのに対し,角度については足し算になっていることです.$\cos$ と $\sin$ の () の中が足し算になっていることを確認してください.
複素数の逆数
複素数は,実数同様に逆数を定義することが出来ます.地味に複素数の重要なところです.
何故重要かというと,逆数…つまり $\frac{1}{x}$ が出来れば割り算ができるからです.
ベクトルや行列は,複数の数を束ねただけなので逆数と言われても困ってしまいます.実際,これらの数について割り算 (掛け算も) は必ずしも出来るとは限らず,計算可能であるために条件が必要になってしまいます.
その点,複素数は割り算が簡単にできます.
これにより,表現の幅であったり計算の利便性が更に高くなります.複素数の場合,割り算,即ち逆数との乗算は角度の引き算をすることに対応します.
複素平面の掛け算の意味
複素平面で掛け算をすることは,角度の足し算を意味することが分かりました.つまり回転です.
これの何がうれしいかって言うと, 計算が超楽になる事です.基本的に,数学では掛け算より足し算の方が扱いやすいので,掛け算を足し算に変換できる性質は重宝されがちです.
対数 ($\log$) なんかがそうでしたね.実際,統計をやる際とかに,掛け算はややこしいので足し算の形に表したいという理由で関数を対数関数に変換する作業なんかがよく出てきます.
そしてこの性質が今後とても大事になるオイラーの公式というものに結びついているのです. しっかりと理解しておきましょう.
オイラーの公式
証明は今の段階では難しいので紹介だけになりますが,オイラーの公式をここで確認しておきます.
オイラーの公式は脳波解析の基本の基本,全てにおいて重要になる公式です.基礎数学編における主な目的は,この公式を理解することであるといっても過言じゃない程のものです.まずは確認してみましょう.
$\theta \in \mathbb{R}$ について,
\[\mathrm{e}^{i\theta} = \cos \theta + i\sin \theta\]である.また,$\theta=\pi$ の時,
オイラーの等式
\[\mathrm{e}^{i\pi} +1= 0\]が成り立つ.
三角関数 $\cos, \sin$ の足し合わせが,指数関数 $\mathrm{e}$ の形で表されてますね.また,何やら虚数単位 $i$ もいます.
更にオイラーの公式の特殊形として,オイラーの等式が存在します.
\[\mathrm{e}^{i\pi} + 1 = 0\]美しいですね.数学の基本である指数関数,虚数,三角関数などといったものが濃縮され,数も基本の $1$ と $0$ のみでまとめられています.
この公式が何故重要になるのかは,まだ分からないと思います.また,何故成り立つのかも全く分からないことでしょう.
基礎編の以降のページは2章以降は統計以外の全てが,このオイラーの公式を証明するために必要な数学のおさらいになります.証明はフーリエ変換の方に記載しています.そこでしっかりと理解し,使いこなせるように,もう少しの間基礎の確認を続けていきます.まずは三角関数のおさらいからです.
(尚,それ以外にも,より発展的な解析や信号処理,統計,計算論的神経科学の内容に必要になってくることも多いので,脳波解析以外にも結局必要になる内容ばかりです)