01確率分布

このページでは，様々な確率分布の概形や性質，式について確認します．

基礎編に乗っているような基礎統計量だけの議論では必要ないため，(多分)高校数学ではやりませんが，それ以上の統計学をやる上で必須になってくるのが確率分布の概念です．

少々面倒ですが，中には非常に重要なものもあるのでしっかり確認しておきましょう．

• はじめに
• 確率分布と確率密度関数
• 一様分布/ベルヌーイ分布/2項分布/ポアソン分布
  • 一様分布
  • ベルヌーイ分布
  • 2項分布
  • ポアソン分布
• 正規分布
  • 正規分布とは
  • 確率密度関数の導出
  • 100p%点
• t分布
• $\chi$二乗分布
• F分布
• 最後に

はじめに

世の中には無数の統計的データがある，というか収集できますが，それらの統計的な分布，つまりヒストグラムの形は概ねいくつかの典型的なパターンのどれかに当てはまる事が知られています．

中でも正規分布という分布は重要で，中心極限定理という定理が示すように世の中の多くの事象に適用できる分布の形です．

これらについて知っていると，その性質から考えて，

• 実際に得られたデータの平均や分散といった値はどうなのか（推定）
• そもそも普通にありえる話なのか，何か特殊な事情で一般的ではないデータが取られたのか（統計的検定）
• 次にどのような振る舞いをするか（予測）

など，様々な議論を展開していく事が可能になります．

そのため，確率分布はそれだけで学んだところで特に面白味がありませんが，今後使っていくという意味では重要です．ここでは，代表的な確率分布を載せていきます．覚える必要はないので，どんな奴らがいるのかなんとなく見て，これ以降の議論で出てきた際に参照できるようにしておきましょう．

たとえばですが，有名な統計的仮説検定であるt検定に使う分布はt分布，F検定に使う分布はF分布，といった具合に，つどつど必要になってくる知識になります．

確率分布と確率密度関数

まずは定義の確認から改めて行っておきましょう！

確率とは, 起こりうる全体の事象のうち, ある事象がどれくらいの割合で起こるのかを表します.

確率分布とは, 起こりうる事象それぞれの確率がどのような分布をしているかです.

確率密度関数とは, 実際に確率分布をプロット(横軸に事象, 縦軸に確率)した際に現れる分布の形を表現する関数の事です. 場合によっては事象は離散分布になったりするため，その場合はこの分布を連続と見立てて確率密度関数が定義されます．

一様分布/ベルヌーイ分布/2項分布/ポアソン分布

まずは簡単な分布から見て, 徐々に複雑なものを見ていきます. 基本的なものについては，まとめて雑に確認します.

一様分布

例えばサイコロを振った時に出る目の確立分布を考えると, 当然6つの事象それぞれがすべて$\frac{1}{6}$で表せるため, プロットすると以下のようになります.

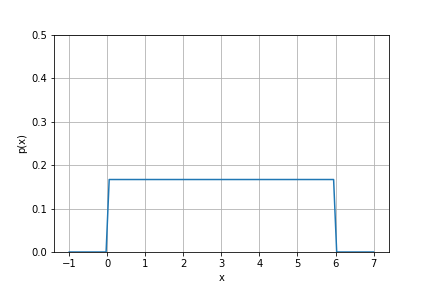
一様分布は確率密度関数を定義するまでもないのですが, 勉強のためにあえてやるとすると以下のようになります. まずさいころの例だとそれぞれの目が出てくる確率はこうですね．

$$f(x) = \frac{1}{6} (1 \leq X \leq 6)$$

1から6の数字が, いずれの点においても$\frac{1}{6}$の確立で目がでるよってことですね. 簡単です.

また確率を考える際, 上の式のように左辺の$(x)$と右辺定義域内にいる$(X)$で使い分けがなされます. $X$は確率変数ですので，観測されて確定した時には$x$として表現されます. 今回の$X$と$x$の関係は

$$X = [x_1, x_2, x_3, x_4, x_5, x_6]$$

のような感じです.

より一般には離散一様分布に従う変数の確率関数は，Nを変数が取りうる値の数(さいころの目=6)として，

$$P(X=x) = \frac{1}{N} \qquad (x=1,2,...,N)$$

と表すことができます．

離散一様分布の期待値と分散は以下です．

$$\mathbb{E}(X) = \sum_{k=1}^N{kP(X=k)}\\ =\sum_{k=1}^N{k\frac{1}{N}}\\ = \frac{(1+N)N}{2}\frac{1}{N}\\ = \frac{1+N}{2}$$

$$\mathbb{V}(X) = \mathbb{E}(X^2) - \mathbb{E}(X)^2\\ = \sum_{k=1}^N k^2 \frac{1}{N} - {(\frac{1+N}{2})}^2\\ = \frac{1}{N}N\frac{(N+1)(2N+1)}{6}-\frac{(N+1)^2}{4}\\ = \frac{N^2-1}{12}$$

一見複雑な気もするかもしれませんが，普通に計算してみればわかるとおもいます．

連続一様分布については確率密度関数は以下のようになります．

連続一様分布

確率密度関数
$$f(x) = \left\{ \begin{array}{l} \frac{1}{b-a} \qquad \qquad (a \leq X \leq b) \\ 0 \qquad \qquad \qquad(otherwise) \end{array} \right.$$

期待値
$$\mathbb{E}(X) = \frac{a+b}{2}\\$$

分散
$$\mathbb{V}(X) = \frac{(b-a)^2}{12}$$

これは面積で考えると分かりやすいかもしれません．

まず，確率密度関数は積分すると1にならないといけません．確率なので自明ですね．

b-aは定義域です．確率密度関数と座標軸で囲まれた部分の面積を考える時，この長さを横の長さと捉えてみましょう．

縦の長さはそれぞれの値が観測される確率，つまり$f(x)$になります．

なので$f(x)$を定義域で積分すると1になります．当たり前の事なのですが，確率密度関数の考え方にいまいち慣れていない人ように丁寧に言いました．以下はこのような話は省略します．

とにかく，積分すると1になるのが確率密度関数です．

一応，期待値くらいは証明もしておきます．でもまあ簡単です．

$$\mathbb{E}(X) = \int_{-\infty}^{\infty} xf(x) dx \\ = \int_{-\infty}^{a} xf(x) dx + \int_{a}^{b} xf(x) dx + \int_{b}^{\infty} xf(x) dx \\ = 0 + \int_{a}^{b} x\frac{1}{b-a} dx + 0\\ = \frac{1}{b-a}\left[\frac{x^2}{2}\right]_a^b\\ = \frac{b-a}{2}$$

ベルヌーイ分布

ベルヌーイ分布は, 1か0のどちらかの値を取る分布です. ある事が起きるか起きないか, 成功するかしないかなどの2値分類ですね.

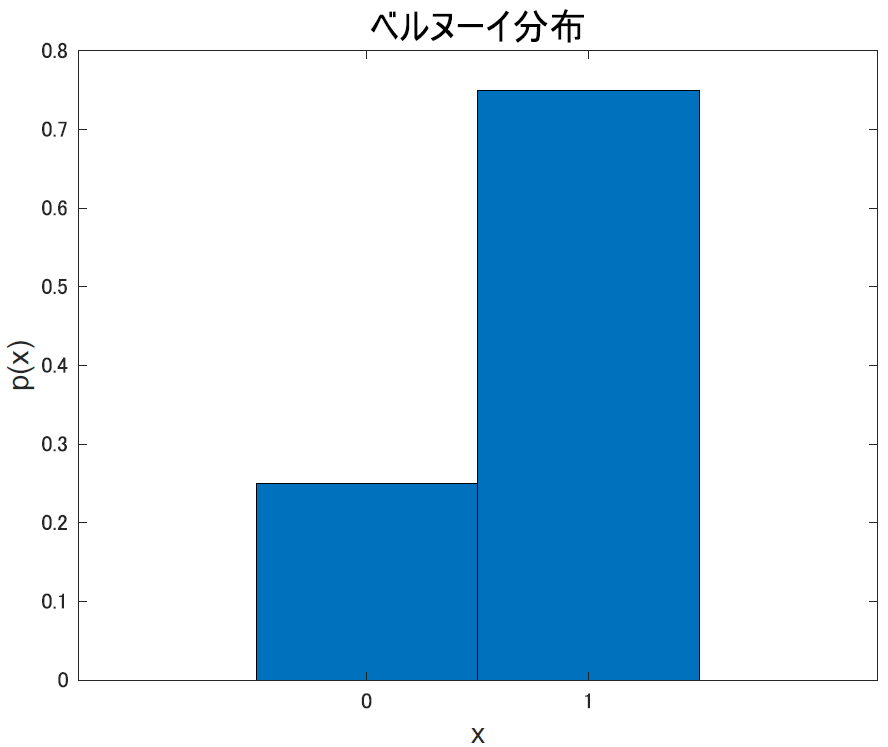
この図では成功が1，失敗が0として成功率75%の何かをやらせたときの確率分布です．他にも，たとえばサイコロで1が出るか出ないか（2や3は区別しない）とか，そんな問題もこの分布で考えられます．

ベルヌーイ分布

確率質量関数
$$f(x)= \left\{ \begin{array}{l} p \qquad \qquad \qquad (x = 1) \\ q(=1-p) \qquad (x=0) \end{array} \right.\\ \text{あるいは}\\ f(x=k) = p^k(1-p)^{1-k}, \quad (k=0,1)$$

期待値
$$\mathbb{E}(X) = p$$

分散
$$\mathbb{V}(X) = pq$$

です. ベルヌーイについては単純なので，このくらいにしておきます．

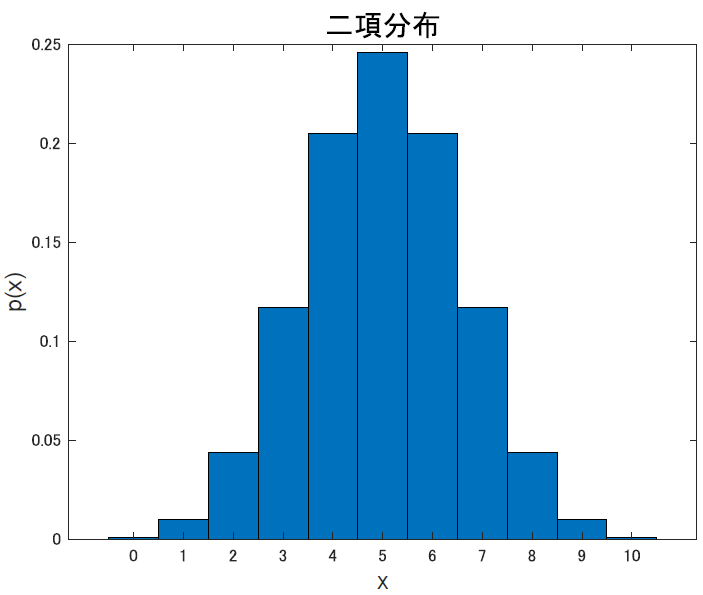
2項分布

２項分布は「同じことを何回も繰り返した時, ある事柄が何回おこるか」の確立分布です. こいつは式を見れば早いですね.

2項分布

確率密度関数
$$f(x) = {}_n\mathrm{C}_x p^x(1-p)^{n-x}$$

期待値
$$\mathbb{E}(X) = np$$

分散
$$\mathbb{V}(X) = np(1-p)$$

式の右辺左側にある${}_n\mathrm{C}_x p^x$は, 確率$p$で起こる事象Aが, 全体$n$のうち$x$回でたという意味で, 右側の$(1-p)^{n-x}$は確率$(1-p)$で, Aが起きなかった回数が$(n-x)$回出たという意味です.

これらを掛け合わせているので, 何回当たって何回外れたかを表す式ですね.

ポアソン分布

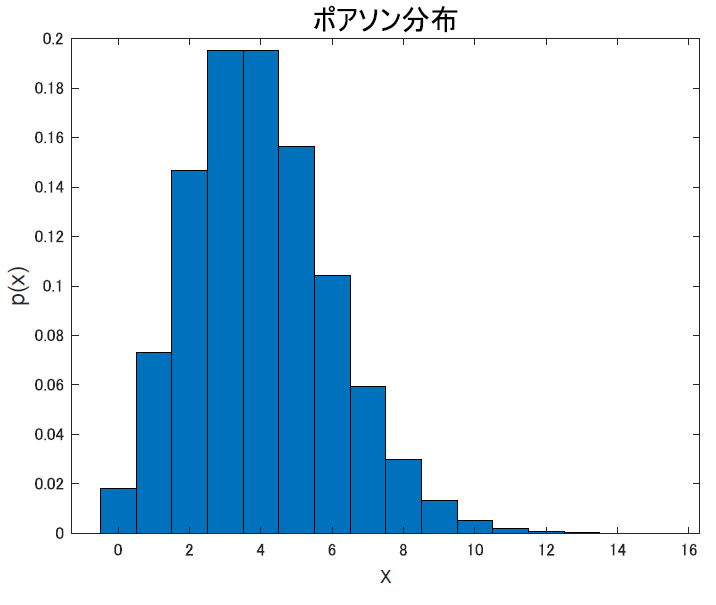
ポアソン分布は「稀な事象が一定時間内にどれくらい起きるか」を表すような分布です.

たとえば, ある月にある地域で起きた交通死亡事故の件数とかです. 愛知県でもない限り, 普通は0か多くて2件とかですよね．多分．

ポアソン分布

確率密度関数
$$f(x) = \frac{\lambda^x}{x!}e^{-\lambda}$$

期待値
$$\mathbb{E}(X) = \lambda$$

分散
$$\mathbb{V}(X) = \lambda$$

です. こいつの場合, 平均も分散も同じ定数$\lambda$なので, こいつの値だけで形が決まります. $\lambda$がどんな値なのか, どうやって決まるのかといったところまでは勉強できていません. 必要を感じることがあれば足します.

正規分布

正規分布とは

さて本題です. 数ある確率分布の中でも抜きんでて重要な分布, 正規分布, またの名をガウス分布です. 世の中の多くの事象がこの分布に従っていて, また従っていると仮定して統計的処理がされています. 今後の統計学を勉強していく上での基礎になるのでしっかり理解しましょう.

正規分布は, 平均$\mathbb{E}(X)$が母集団の平均$μ$と等しく, 分散$\mathbb{V}(X)$も母集団の分散$\sigma ^2$と等しくなる分布で, 確率密度関数は以下になります.

$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

いや, うん. 分かります. やばそうですよね.

ただまぁ, なんでこんな殺意高めな式になるのかは正規分布のグラフを見れば理解できます. 母集団の平均が50, 標準偏差20の正規分布だとこうなります.

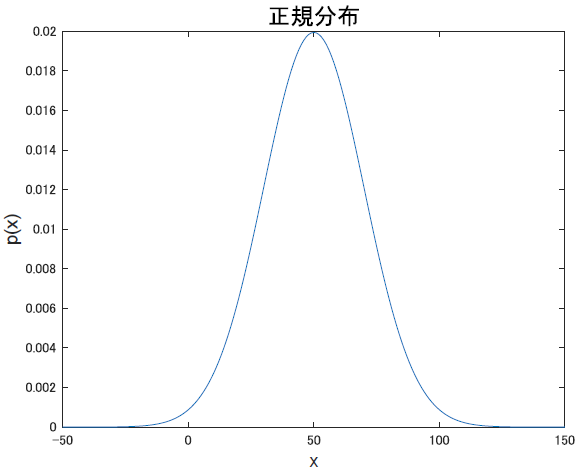
定義通り, 確率変数の平均も50, 分散も400(20の二乗)になっていますね！！これが正規分布です. 綺麗ですね.

確率密度関数の導出

さて, 比較的分かりやすい形をしている正規分布ですが，確率密度関数の式はちょっと複雑に見えます．何故このような形になるのか考えてみましょう. まずややこしいとこを全て消し飛ばし, 以下のように変形しましょう.

$$f(x) = e^{-x^2}$$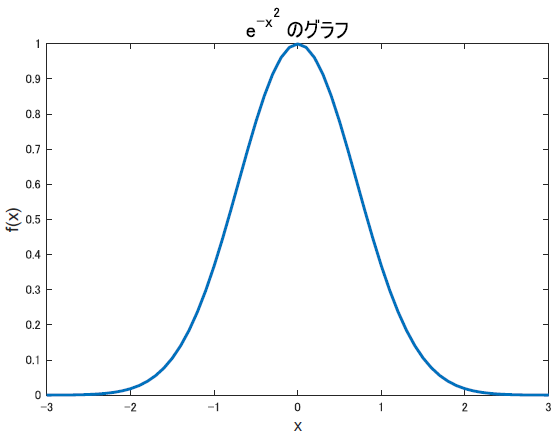

この関数の説明はいりませんね．指数関数の二乗の負版です.

まず, 世の中の多くの事象は平均値を取る確率が一番大きく, 平均値から離れるにつれその値を取る確率は小さくなることが知られています. んで, これをどう数式で表現すれば良いかと悩んだ末考えだされたのが正規分布関数だと思ってください.

そうすると, とりあえず釣り鐘型の関数が欲しくなります．ということでこの式を考えました. 実際これでほぼ完成です.

ただ, これは任意定数がないため平均が0, 分散(幅)も一定ですね. これでは実用できません. そこで任意定数を導入し, 平均値と分散を可変にします.

まずは平均値, つまりこのグラフの頂点の位置を動かします．

$$f(x) = e^{-(x-\mu)^2}$$

高校数学で二次関数の頂点を移動する時にやった操作に似ています.

次に, 分散...つまりこの釣り鐘の幅というか広がり方を変えます.

$$f(x) = e^{-\frac{(x-\mu)^2}{\sigma^2}}$$

平均に比べると，すこし難解かもしれません. σ, つまり標準偏差で割る事で, σの値が小さければ鋭く, 大きければ扁平なグラフになります．

ただ, σは正負が定まらないため, 二乗して分散の形にする事で符号を一定にするわけです.

ともあれ ... これで, 平均と分散によって形を変える釣り鐘型分布が完成です！！めでたい！！

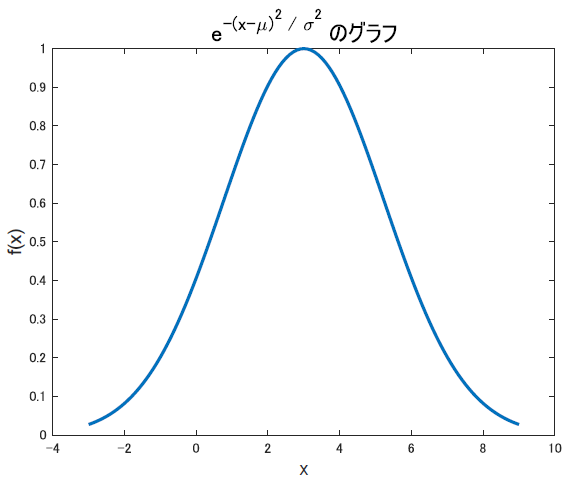
しかし，これでは最初に確認した正規分布の式と違います．

$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

残りの部分はなんなのでしょう．

実際のところ，グラフの形はこれで完成です．釣り鐘型で，平均や分散で操作できる良い感じのグラフが描けています．

では何が足りないのかというと，今我々が求めていたのは正規分布の「確率密度関数」だったということです．

確率の密度なのですから, 当然合計して1にならないといけません．先程の式

$$f(x) = e^{-\frac{(x-\mu)^2}{\sigma^2}}$$

ではその点がダメなのです．ちゃんと全確率点での値を足して1になるように正規化する必要があります．

というわけで積分方程式を解きますがその前に, 出てくる計算結果を綺麗にするために式に細工をし, $\sigma^2$を$2\sigma^2$にしておきます.

$$f(x) = e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

2が付きましたが, グラフの性質自体は変わりません．

では積分方程式.

$$\int_{-\infty}^{\infty} c e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx= 1$$

を解きます...出来たものがこちらです.

$$c = \frac{1}{\sqrt{2\pi\sigma^2}}$$

こうして得られたcを改めて式

$$f(x) = e^{-\frac{(x-\mu)^2}{\sigma^2}}$$

の係数として反映すると

$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

このように，ようやく正規分布の確率密度関数が求まりました．

以上が正規分布の確率密度関数の導出工程でした. とは言っても，これは結構邪道な求め方な気がします．釣り鐘型から天下り的に作っているし．もう少し自然な導出の仕方などはあるようですので，気になる方はそちらを確認してみてください．

とにかくここで重要だったのは，正規分布とは世の中によく存在する「釣り鐘型の分布」を良い感じに表現する分布で，それを表現するためにちょっと複雑に見える式の形をしていたのだ，ということです．

100p%点

次に100p%点についてです．

正規分布を学ぶ意味は, この概念があるからといっても過言じゃない重要な性質です.

正規分布は平均が丁度真ん中で, 広がり方は分散によって定義される左右対称な特殊な分布でしたね．つまり, 平均の周辺であるほど高確率で観測され, 裾野ほど「レア」な事象というわけです.

この性質を利用して, (標準)正規分布には「100p%点」と呼ばれる指標を導入する事が出来ます. これは「その点以上(以下)の部分の確率の合計がpになる境界」を指します. x軸の正方向なら上側, 負方向なら下側, 両方を指すなら両側100p%点です.

この便利な点について考えていきます．まず標準正規分布とは異なる平均値や分散値を持っている正規分布を同じ土俵で比べるために平均0，分散１に揃える操作，標準化をした正規分布の事でした．

なので標準正規分布において定義される100p%点は，どんなデータであろうと正規分布に従っているのであれば対等に語れる点である事が分かります．

これを使うからこそ，有名なt検定だとかを使った時にp値が0.05だ～とかそんな話ができるわけです．

言葉だとややこしいですが, グラフで見れば一瞬で分かります.

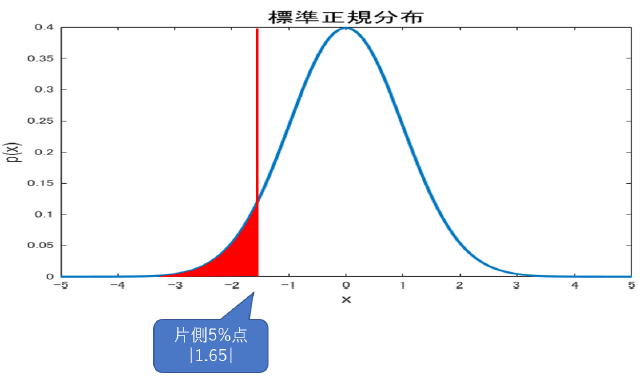
こちらが片側（下側）5%点で，

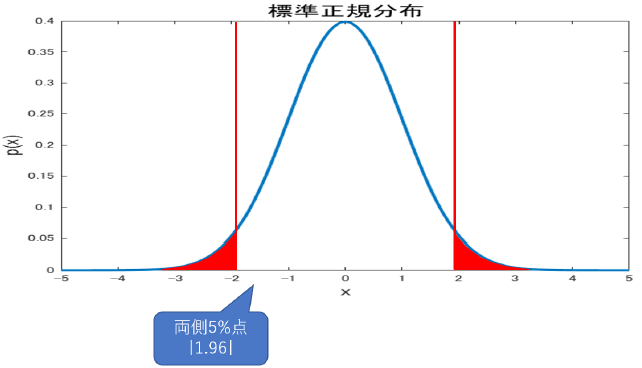
こちらが両側5%点になります．

下側5%に比べ, 両側5%は左右に領域が分散した分上側の領域が狭くなってるのに注意です.

だいたい, 正規分布でよく用いられるのは上下両側の5%と1%点です. 何に使うのかはあとで説明するので, ひとまず概念だけ覚えておいてください.

t分布

少ない標本数をもとに母分散がわかっていない母集団の母平均推定に使われるのがt分布です. 詳しくは推定の項で触れるので, ここでは確率密度関数と性質の確認をします.

$$f(x) = k(1 + \frac{x^2}{\alpha})^{-\frac{\alpha+1}{2}}$$

これがt分布の確率密度関数です. ここで$k$は定数, $\alpha$は自由度という指標で, この形を「自由度$\alpha$のt分布」と表現します. 自由度とは何かはここでは説明しませんが, 母集団によって算出できる値です. 自由度の値によって，定義される確率密度関数の形は変わります．それ以外の部分では正規分布に似ていますね. 実際, 自由度$\alpha$が十分に大きい場合には正規分布になります.

しかし，平均と分散は

$$\mathbb{E}(X) = 0\\ \mathbb{V}(X) = \frac{\alpha}{\alpha-2}$$

です.

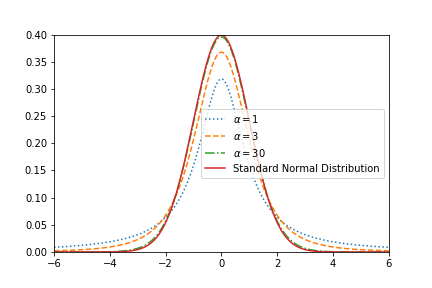
上の図は自由度の異なるt分布と標準正規分布の比較です. 標準正規分布とは, 正規分布のうち平均が0, 分散が1のやつです. $\alpha$の値が大きいとほぼ同じ形になる事が分かると思います.

では何に使うのかですが, 有名なt検定などになります．が，今はそこはひとまず置いておきます. とにかくこういう分布があるのです.

$\chi$二乗分布

次に，$\chi^2$分布について確認します. こいつも重要です.

$\chi^2$分布

独立に標準正規分布に従うk個の確率変数${X_1, ..., X_k}$を考えた時，これに対する統計量

$$Z = \Sigma_{i=1}^{k} X_i ^2$$

が従う分布のことを，自由度$k$の$\chi^2$(カイ二乗)分布．

確率密度関数
$$f(x) = \frac{1}{2^{\frac{k}{2}}\Gamma(\frac{k}{2})}(x^2)^{\frac{k}{2}-1}e^{-\frac{x^2}{2}}$$

期待値
$$\mathbb{E}(X) = k$$

分散
$$\mathbb{V}(X) = 2k$$

我々は実験の結果を理論やモデルに落とし込む時, なんらかの数式に近似したり回帰したりするわけですが, 実際問題理論と観測値が完全に一致するなんていう事はまれで, 様々な要因で若干の誤差が生じます.

得られた誤差が「誤差」なのか「理論の誤り」なのかを評価する時に使ったりするのがこの分布とそれに基づく検定です. ピアソンのカイ二乗検定なんていうものなんかがそうですが，その説明はまた今度です．

確率密度関数を見ると分かりますが，かなり不思議な分布になります．また確率密度関数の途中で出てくる$\Gamma$はガンマ関数

$$\Gamma(\frac{k}{2}) = \int_0^\infty t^{\frac{k}{2}-1} e^{-t}dt$$

です．かなり複雑になりますね．しかし実際のところ，この式自体はそれほど使う事がないというか，覚える必要がなさそうなので紹介に留めておいておきます．

大事なのはグラフの見た目です．たとえば，自由度$k=4$の時の$\chi^2$分布は以下のようになります．

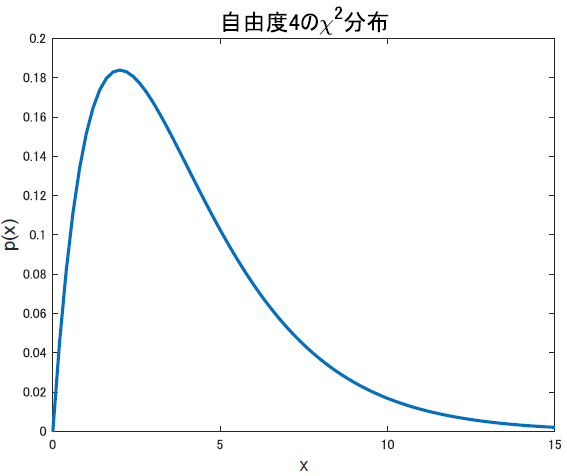
上は一例ですが，t分布同様に自由度によって形が変わるので，他の自由度の場合を見比べてみると以下のようになります．

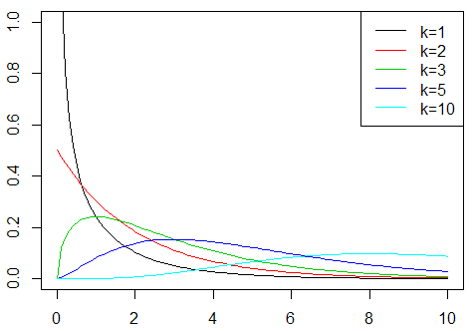
かなり変わることが分かるかと思います．

F分布

最後にF分布について確認します．

F分布は, 少し特殊な形をしていますが非常に重要です. どう重要かというと，これまでの分布と異なり, ２つの母集団から得られた標本分散の比の確率分布になります．これによって，分散分析，ANOVAと呼ばれる統計的検定に使うことになるので，しっかりと確認しておきます．

先に見た目を確認します．たとえば，自由度3,5のF分布をプロットしてみると以下のようになります．

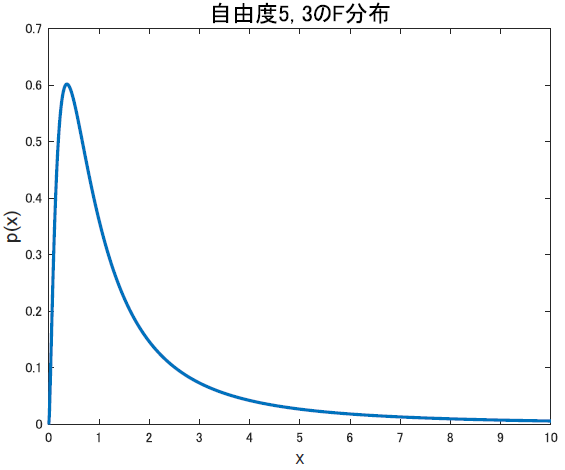
さて，定義を確認します．

F分布

自由度$k_1, k_2$のカイ二乗分布が互いに独立であるとき，

$$F = \frac{\chi_1^2/k_1}{\chi_2^2/k_2}$$

が従う確率分布．

確率密度関数
$$f(x;k_1, k_2) = \frac{\Gamma(\frac{k_1 + k_2}{2})x^{\frac{k_1-2}{2}}}{\Gamma(\frac{k_1}{2})\Gamma(\frac{k_2}{2})(1+\frac{k_1}{k_2}x)^\frac{k_1+k_2}{2}}(\frac{k_1}{k_2})^{\frac{k_1}{2}}$$

期待値
$$\mathbb{E}(X) = \frac{n}{n-2} \quad (n > 2)$$

分散
$$\mathbb{V}(X) = \frac{2n^2 (m+n-2)}{m(n-2)^2(n-4)} \quad (n>4)$$

$$f(x) = \frac{kx^{\frac{m}{2}-1}}{\{1 + (\frac{m}{n})x\}^{\frac{m+n}{2}}}$$

かなり複雑な形をしていますし，式については諦めます．

重要なのは，2つの自由度をもつ分布の関係性を表す「自由度$k_1, k_2$のF分布」というものがある，ということです．

等分散性の検定，それを使った分散分析などに重要になってくる分布です．

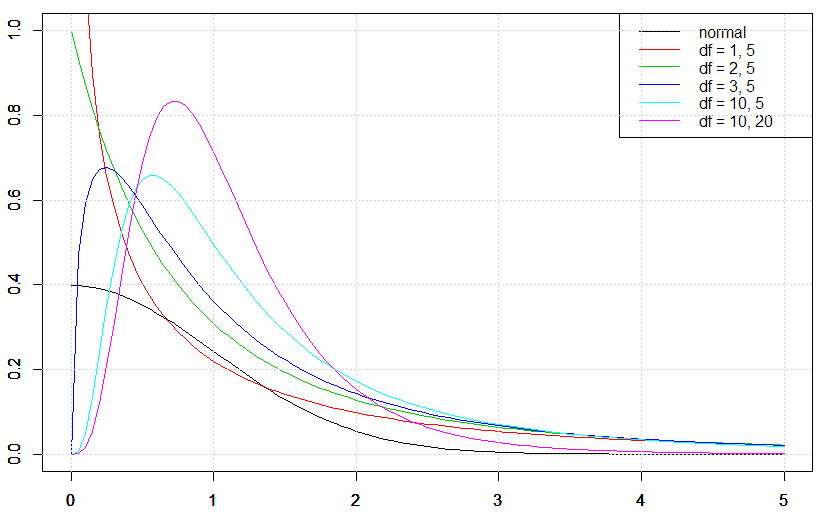
こちらも，やはり自由度によって振る舞いがかわります．

最後に

以上で，確率分布の確認をとりあえず終わりとしておきます．実際にはここに載せた以外にもたくさんの分布がありますし，それぞれについて重要な性質であったり使い方はやはりたくさんあります．

勿論，ここに載せた分布についても説明が不十分な点は多々あります．

しかし，何に使うのかも分からない状態でやらされる勉強ほど面白くないものはないので，ひとまずはこのへんにしておきます．

今後，統計的仮説検定だったりといった操作についてまとめる過程で，足りない情報は適宜補充していこうと思っています．

Math 基礎数学編 掛け算 三角関数 複素数 微分・積分 基礎統計 信号処理編 フーリエ変換 wavelet変換 ヒルベルト変換 基本の脳波解析 位相同期解析 統計編 確率分布 大数の法則と中心極限定理 統計量と標本分布 統計的検定 分散分析	Analysis EEGLAB 環境構築 データのインポート 基本的な下処理 発展的な下処理 単被験者での解析 被験者群での解析	Experiment 基礎数学編 掛け算 三角関数 複素数 微分・積分 基礎統計 信号処理編 フーリエ変換 wavelet変換 ヒルベルト変換 基本の脳波解析 位相同期解析	Simulations 環境構築 Python環境構築 pythonでのGPUセットアップ Jupyterセットアップ Juliaセットアップ