03ヒルベルト変換

フーリエ変換とウェーブレット変換が理解できれば，ひとまず時間周波数解析の話は出来るようになります．ここでは，これらに比べると少し特殊ですが同様によく使う変換である，ヒルベルト変換について確認します．

• ヒルベルト変換のモチベーション
• ヒルベルト変換

ヒルベルト変換のモチベーション

フーリエ変換やウェーブレット変換はもともと実部しか存在しない元信号を複素サインと内積していく事で複素数として返す性質を持っていました．これによるメリットはいくつかあります．

まず，特定の複素サイン$(\omega 0)$との積の実部は「元信号に含まれる$\omega 0$成分」を表します．実部と虚部を使ってだす絶対値は瞬時の振幅を，そしてその振幅によって定義される時系列を包絡線と言いました．

虚部を算出する最大のメリットは，瞬時位相，振幅を出せるところにあります．位相と振幅の出し方は基礎でやりましたね．

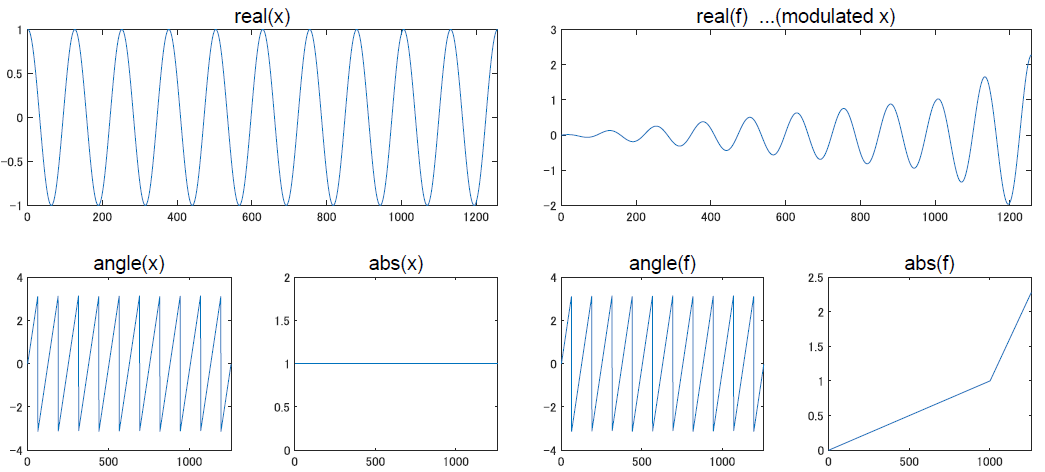
たとえば上の図では，左側は普通のサイン波から取り出した瞬時の位相と振幅，右側は振幅が時間発展するサイン波から取り出した位相と振幅をプロットしてみました．

振幅と位相は独立しているので，右の図のような変な波形相手でも位相は左側と変わっていません．

さて，本題です．フーリエ変換やウェーブレット変換の時，周波数分解したものをプロットすると負の周波数も存在していたのを覚えているでしょうか．解説の際には，負の周波数は解析的に出てきちゃうもので無視して良いと言いました．こういう意図的に無視する，とかじゃなく元信号に対しなんらかの変換を通して，負の周波数を除いて再構成された波の事を解析信号と言います．その解析信号の出したいと考えるとき，必要になるのは

$$f(t) = A\cos\omega t\rightarrow A(\cos\omega t + i \sin\omega t)$$

とする変換を考えれば良いわけです．これがヒルベルト変換のモチベです．

ヒルベルト変換

モチベーションが分かったところで，早速式を見てみます．

$$H(f)(t):= \frac{1}{\pi} \int_{-\infty}^\infty \frac{f(t)}{t-\tau} d\tau$$

元関数と$\frac{1}{\pi t}$との畳み込みっぽいですね．しかし残念，筆者はこの式がどっから来てるのかとかはよく知りません．ごめんなさい．

この式は周波数領域においてはもっと単純で分かりやすい変換となり，それが以下の式で表されます．

$$F(H(f(\omega))) = (-i sgn(\omega))F(f(t))(\omega)\\ \text{ただし} -i sgn(\omega) = \begin{cases} i=e^{i\pi/2} & for \omega<0\\ 0 & for \omega = 0\\ -i = e^{-i\pi/2} & for \omega > 0 \end{cases}$$

$F$はフーリエ変換です．つまり，元信号$f(t)$をフーリエ変換した結果$F(f(\omega))$に$-sgn(\omega)$をかけたものが，ヒルベルト変換したもの$H(f(\omega))$をフーリエ変換したものと等しい，という関係です．

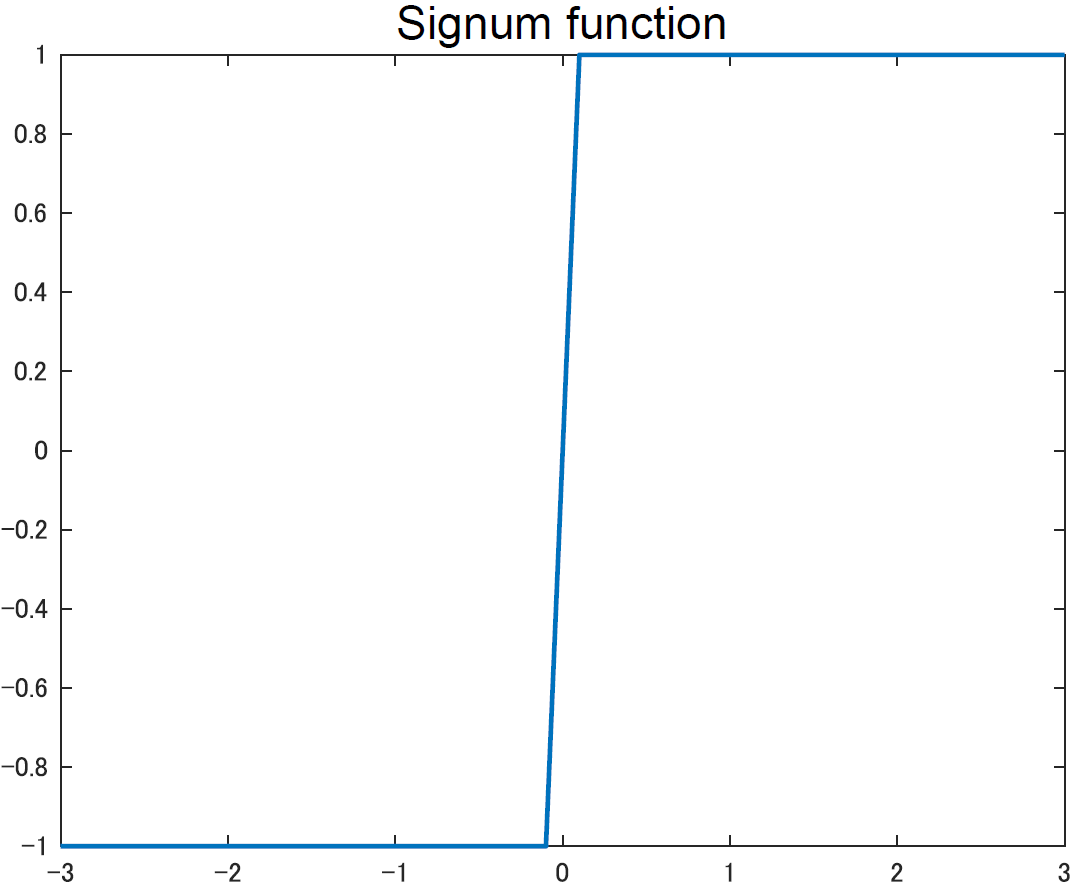
$sgn$関数，符号関数は$sin$と名前が似てますが全くの別物で，xが0未満だと-1, 0の時0，0より大きいと1という値を取ります．

%% signum function
x2 = -3:0.1:3;
plot(x2, sign(x2), 'LineWidth', 1.5)
title('Signum function', 'FontName','Arial', 'FontSize', 15)

なんでこの式によって解析信号が得られるのか，オイラーの公式を使って考えていきましょう．

はじめに，実信号として得られた角周波数($\omega_0$)の実信号$f_1$があったとします．

$$f_1(t) = A \cos(\omega_0 t)$$

こいつを，とりあえず$-\pi/2$だけ位相シフトさせます．すると

$$f_2(t) = A \cos(\omega_0 t - \frac{\pi}{2}) = A \sin(\omega_0 t)$$

こうなりますね．cosをsinに変換しました．さらに，こいつに$i$を乗じたものを元の$f_1$に足すと

$$f(t) = f_1(t) + if_2(t) = A(\cos(\omega_0 t) + i \sin(\omega_0 t))$$

となります．これはオイラーの公式を使うと$e^{i\omega_0 t}$で表せます．正の周波数$\omega_0$を含みつつ，負の周波数は含んでないので解析信号になります．最初からオイラーの公式で再現してみましょうか．

$$f_1(t) = A(\exp(i\omega_0 t) + \exp(-i\omega_0 t))/2 \nonumber \\ f_2(t) = -iA(\exp(i\omega_0 t) - \exp(-i\omega_0 t))/2$$

オイラーの公式からこう表せますよね．納得できない人は実際に計算してみてください．こう表すと，両方とも負の周波数$-\omega_0$を含んでいる事が分かるかと思いますが，これを先程と同様に足してみると

$$f(t) = A(e^{i\omega_0 t} + e^{-i\omega_0 t})/2 + i(-iA(e^{i\omega_0 t} - e^{-i\omega_0 t}/2)) = A e^{i\omega_0 t}$$

となります．たしかに負の周波数が消えて$e^{i\omega_0 t}$がとれていますね．

ということで，たしかに負の周波数は$i$，正の周波数は$-i$をかけたものをうまく使う事で解析信号が取り出せる事が分かりました．

こうして作成した信号を正の周波数とし，負の周波数はなくして(0にして)逆フーリエ変換にかければヒルベルト変換の完成です．コード見てみれば理解も深まると思います．

%% hilbert
fs = 100;
t = -pi:1/fs:pi;
n = length(t);
x1 = cos(5*t);
x2 = x1 + cos(t) + cos(20*t);
y1 = fft(x1);
y2 = fft(x2);

posF = 2:floor(n/2)+mod(n,2);
negF = ceil(n/2)+1+~mod(n,2):n;

% 負の周波数はいらない
yhilbert1(negF) = 0*y1(negF);
yhilbert2(negF) = 0*y2(negF);

% 正の周波数expと負の周波数exp (iがけした) を足したものを新しい正の周波数に
yhilbert1(posF) = (y1(posF) + y1(negF)) + 1i*(-1i*(y1(posF) - y1(negF)));
%yhilbert(posF) = (y(posF) + y(negF)) + 1i*(-1i*(y(posF) - y(negF)));


% つまりは単純に二倍
%yhilbert1(posF) = 2*y(posF);
yhilbert2(posF) = 2*y2(posF);

% 逆フーリエ
H1 = ifft(yhilbert1);
H2 = ifft(yhilbert2);

subplot(3,2,1)
plot(t, x1)
title('sine wave', 'FontName','Arial', 'FontSize', 15)

subplot(3,2,2)
plot(t, x2)
title('combined sine wave', 'FontName','Arial', 'FontSize', 15)

subplot(3,2,3)
plot(t, real(H1), t, imag(H1))
title('Handmade HT', 'FontName','Arial', 'FontSize', 15)
legend('real','imag','FontName', 'Arial', 'FontSize', 10 ,'Location','Best' )

subplot(3,2,4)
plot(t, real(H2), t, imag(H2))
title('Handmade HT', 'FontName','Arial', 'FontSize', 15)
legend('real','imag','FontName', 'Arial', 'FontSize', 10 ,'Location','Best' )

subplot(3,2,5)
plot(t, real(hilbert(x1)), t, imag(hilbert(x1)))
title('Hilbert function', 'FontName','Arial', 'FontSize', 15)
legend('real','imag','FontName', 'Arial', 'FontSize', 10 ,'Location','Best' )

subplot(3,2,6)
plot(t, real(hilbert(x2)), t, imag(hilbert(x2)))
title('Hilbert function', 'FontName','Arial', 'FontSize', 15)
legend('real','imag','FontName', 'Arial', 'FontSize', 10 ,'Location','Best' )

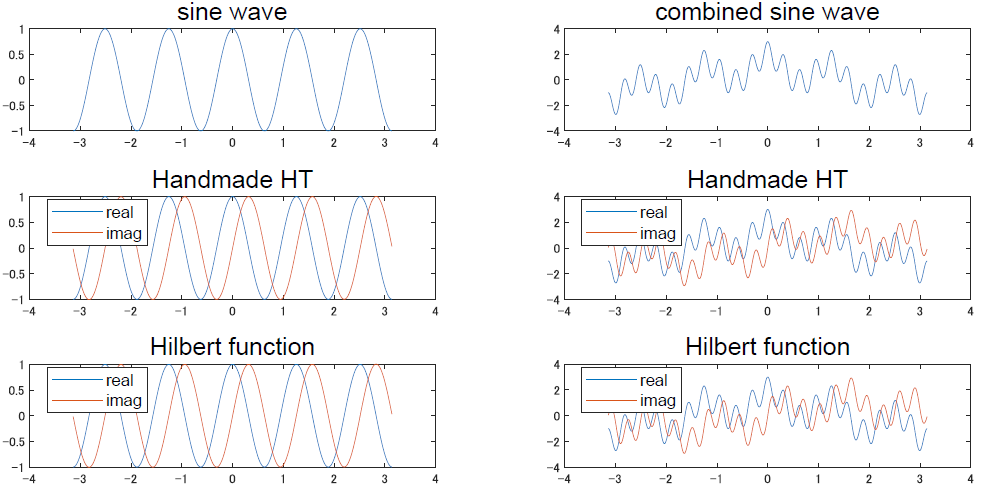
とにかく，こうして解析信号を得られたら後はフーリエの時と一緒で振幅や位相の議論ができるようになります．これ以降に記述していく様々な解析のために重宝するので，覚えておきましょう．